Wordle has gotten popular. A cross between hangman and MasterMind, it’s cute, simple, and competitive. It has all the elements required to go viral. I finally decided to indulge in the clever word game about a week before it was purchased by the New York Times.
Since the New York Times took charge, there have only been minor changes. Some people are claiming that the New York Times has changed the word list, and is favoring more difficult words. There have also been some mishaps where users have gotten different words from each other.
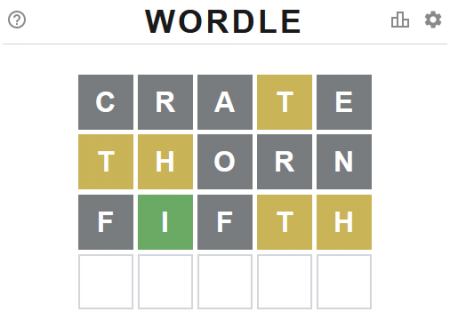
The way Wordle was written, it has a list of 2,315 words completely exposed in the JavaScript code. Each day the next word in the list becomes the word of the day. One of the first words I encountered when playing was “moist,” the 228th word in the list. The next word, “shard,” appeared on the subsequent day, and so on.
I decided I wanted to see how the New York Times had modified the list. First, I had to find the original list. The original site, powerlanguage.co.uk/wordle/, now redirects to the New York Times, so in order to get the unadulterated code, I used the WayBack Machine to look at the site as it appeared before the sale.
The array of words is contained in a JavaScript file. I extracted the array of words from both the old and new, then compared.
6 words have been removed:
- agora
- pupal
- lynch
- fibre
- slave
- wench
Both “agora” and “pupal” are words that should have appeared in the last few weeks. In fact, “pupal” is the word some people got when visiting the original Wordle site on February 19, 2022, whereas the users who visited the new New York Times version got the word “swill” (which is two words later in the list).
Excerpt from original Wordle list
"moist","shard","pleat","aloft","skill","elder","frame","humor",
"pause","ulcer","ultra","robin","cynic","agora","aroma","caulk",
"shake","pupal","dodge","swill","tacit","other","thorn"Excerpt from New York Times list
"moist","shard","pleat","aloft","skill","elder","frame","humor",
"pause","ulcer","ultra","robin","cynic","aroma","caulk","shake",
"dodge","swill","tacit","other","thorn"Since two omitted words have been encountered, the original and new games are now off by two. The next omitted word, “lynch,” won’t be encountered for another 50 or so days (at the time of writing).
Despite the rumors, no words have been added, and the ordering of words has not been otherwise altered.
Since we are on the subject of Wordle, I decided it would be fun to make a utility to help guess the words. It would be too unsporting to just use the word list that the game provides, so I found a list of the most popular English words, and extracted all the five-letter words. This yielded about 3000 words, which is more than the official Wordle list.
I made a simplistic web app that can be used to input the letters and indicate if they appear green or yellow, or not used at all. The app will return a list of possible words for the given configuration.
I don’t condone cheating, and I don’t use this when I play Wordle. It was merely a fun exercise. You can try it out for yourself here.